Turbulence

Our turbulence research focuses on non-equilibrium problems, including, for example, unsteady turbulent flow and buoyancy-influenced turbulent flow. Complementary experimental and computational methods are used.

Off

Experimental studies are carried out using advanced flow measurement techniques, including Laser Doppler Anemometry (LDA), Particle Image Velocimetry (PIV) and hot-film anemometry. Computational studies are carried out using DNS, LES and RANS approaches with computer codes developed and maintained by the group.

DNS, as a major tool used in our recent studies, provides detailed faithful information on the flow which enhances our understanding of the physics as well as providing detailed benchmark data for validation of engineering modelling methodologies.

Nevertheless, DNS (and LES) are currently limited to simple geometry flows at relatively low Reynolds numbers. RANS approaches on the other hand are used to extend the flow conditions studied after carefully designed validation exercises. Experimental studies are used to back-up these numerical simulations.

[Highlight] Laminar or turbulent flow?

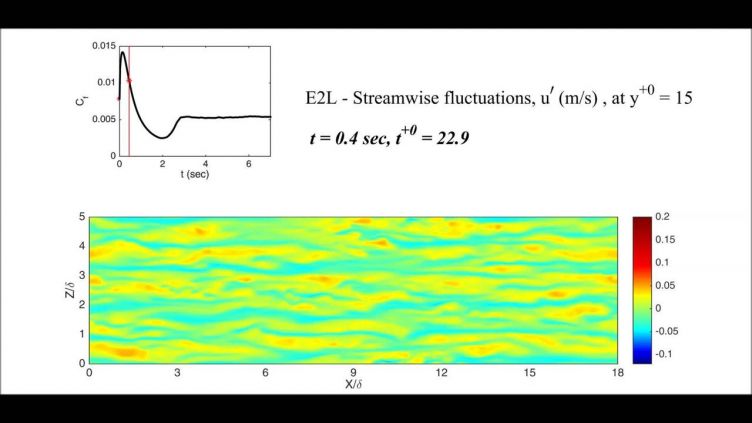
We have recently shown that a transient flow accelerating from an already turbulent state is characterised by the development of a laminar boundary layer followed by transition. See Key research topics.

Research projects

  • Flow laminarisation and drag reduction, PhD project, 2020-2024
  • Turbulence dynamics in spatially accelerating flows, EPSRC CASE PhD Studentship, 2019-2023
  • Fundamental Study of Turbulence in unsteady flows, PhD project, Benjamin Oluwadare, 2015-2018
  • Study of flow and heat transfer of fluids at supercritical pressure using DNS, EPSRC through EP/K007777/1, 2012-2015
  • Effect of body force on turbulent pipe flow, PhD project, Kui He (Tom), 2011-2015 
  • Studies of turbulence in unsteady flow, PhD project, Akshat Mathur, 2012-2015.
  • Turbulence and wall shear stress in unsteady internal flows with rough surfaces EPSRC (EP/G068925/1), 2010-2013.
  • Unsteady friction in pipes and ducts (Hydralab), 2007-2008
  • Theoretical and experimental study of the dependence of transient pipe friction on turbulence dynamics, EPSRC (EP/C015177/1), 2006-2008.
  • Modelling of turbulent heat transfer to fluids at supercritical pressure EPSRC (GR/S19424/01), 2003-2006.

Key research topics

1. Laminar-turbulent transition of transient turbulent flow

Ever since the publication of the pioneering work of Osborne Reynolds in 1883 defining the concept of laminar and turbulent flows, the subject has remained a central theme in fluid mechanics due to its fundamental importance to the subject and its relevance to engineering applications and the natural world. We know, for example, that the flow in a pipe is likely to be laminar when the Reynolds number is below around 2300 and turbulent when the Re is higher.

Recently, we made some ‘surprising’ observations which lead to a radically new interpretation of transient turbulent flows, seemingly deviating from the conventional turbulence theory.

The new findings lead to the following statement: the transient flow following a rapid increase of flow rate from an initially turbulent flow is characterised by a time-developing laminar boundary layer followed by laminar-turbulent transition even though the initial flow is turbulent.

An alternative statement of the finding is that: the transient turbulent channel flow represents a new category of bypass transition, which develops from an established turbulent wall shear flow. This contrasts the conventional boundary layer bypass transition induced by free stream turbulence.

These findings are reported in the following publications:

  1. S. He, M Seddighi (2013), Turbulence in transient channel flow, Journal of Fluid Mechanics, 715, 60-102.
  2. Seddighi M, He S, Vardy AE & Orlandi P (2014) Direct numerical simulation of an accelerating channel flow. Flow, Turbulence and Combustion, 92(1-2), 473-502.
  3. S. He & M. Seddighi (2015) Transition of transient channel flow after a change in Reynolds number, Journal of Fluid Mechanics, 764, 395-427.
  4. Seddighi M, He S, Pokrajac D, O’Donoghue T & Vardy AE (2015) Turbulence in a transient channel flow with a wall of pyramid roughness. Journal of Fluid Mechanics, 781, 226-260.
  5. He K, Seddighi M & He S (2016) DNS study of a pipe flow following a step increase in flow rate. International Journal of Heat and Fluid Flow, 57, 130-141.
  6. Mathur A, Gorji S, He S, Seddighi M, Vardy AE, O'Donoghue T & Pokrajac D (2018) Temporal acceleration of a turbulent channel flow. Journal of Fluid Mechanics, 835, 471-490.
Generation of turbulent spots (fig. 1); streamwise and spanwise turbulence (fig. 2)
Figure (left) shows generation of turbulent spots; Figure (right) shows that the streamwise and spanwise turbulence exhibiting 'discontinuities' at the time of transition in a transient turbulent flow.
2. Flow laminarisation

It is well established that when a turbulent flow is subjected to a non-uniform body force, the turbulence may be significantly suppressed and the flow is laminarised. This is the situation in buoyancy-aided mixed convection when severe heat transfer deterioration may occur.

In contrast to this conventional view, we show that the essential turbulence characteristics including mixing characteristics of the turbulence represented by the turbulent viscosity remain largely unaffected while applying a body force to a turbulent flow while keeping the pressure force unchanged. The so-called flow laminarisation can be viewed as a reduction in the apparent Reynolds number of the flow, value of which can be readily established. Please read:

  1. He S, He K & Seddighi M (2016) Laminarisation of flow at low Reynolds number due to streamwise body force. Journal of Fluid Mechanics, 809, 31-71.
  2. Marensi E, He S & Willis AP (2021) Suppression of turbulence and travelling waves in a vertical heated pipe. Journal of Fluid Mechanics, 919, a17
Flow laminarisation graphs
Figure (left) shows instantaneous velocities in various 'laminarised' flows; Figure (right) shows that turbulent shear stresses of DNS results are well predicted by simply theory assuming turbulent viscosity is not influenced by non-uniform body force.

3. Unsteady flow modelling and experiments

For unsteady turbulent flows, experimental and computational studies have been carried out on accelerating, decelerating and sinusoidal flows over many years. Both smooth and rough walls with 2D and 3D roughness configurations are considered. A selection of publications are listed below:

  1. Vardy AE, Brown JMB, He S, Ariyaratne C & Gorji S (2015) Applicability of Frozen-Viscosity Models of Unsteady Wall Shear Stress. Journal of Hydraulic Engineering, 141(1), 04014064-04014064. 
  2. Gorji S, Seddighi M, Ariyaratne C, Vardy AE, O'Donoghue T, Pokrajac D & He S (2014) A comparative study of turbulence models in a transient channel flow. Computers and Fluids, 89, 111-123.
  3. Seddighi M, He S, Vardy AE & Orlandi P (2013) Direct Numerical Simulation of an Accelerating Channel Flow. Flow, Turbulence and Combustion, 1-30.
  4. Mathur A & He S (2013) Performance and implementation of the Launder–Sharma low-Reynolds number turbulence model. Computers & Fluids, 79(0), 134-139.
  5. S. He, C. Ariyaratne and A.E. Vardy, Wall shear stress in accelerating turbulent pipe flow, Journal of Fluid Mechanics, 685, pp. 440-460, 2011.
  6. M. Seddighi, S. He, P. Orlandi & A. Vardy, A comparative study of turbulence in a ramp-up and a ramp-down flow, Flow Turbulence and combustion, 86 (3-4), pp. 439-454, 2011.
  7. S. He, C. Ariyaratne, Wall shear stress in the early stage of unsteady turbulent pipe flow, J. Hydraul. Eng., 137 (5), pp. 606-610, 2011.
  8. C. Ariyaratne, S. He and A.E. Vardy, Wall Friction and Turbulence Dynamics in Decelerating Pipe Flows, Journal of Hydraulic Research, 48 (6), pp. 810-821, 2010.
  9. S. He and J.D. Jackson , ‘An experimental study of pulsating turbulent flow in a pipe’, European Journal of Mechanics – B/Fluids, Vol. 28, pp309-320, 2009.
  10. S. He, W.S. Kim and J.H., Bae, Assessment of performance of turbulence models in predicting supercritical pressure heat transfer in a vertical tube, International Journal of Heat and Mass Transfer, Vol. 5, pp4659-4675, 2008.
  11. S. He, C. Ariyaratne and A.E. Vardy, ‘A computational study of wall friction and turbulence dynamics in accelerating pipe flows’, Computers and Fluids, Vol. 37, pp674-689, 2008.
  12. W.S. Kim, S. He, J.D. Jackson ‘Assessment by comparison with DNS data of turbulence models used in simulations of mixed convection’, International Journal of Heat and Mass Transfer, Vol. 51, pp 1293-1312, 2008
  13. S. He, Z. Xu and J.D. Jackson ‘An experimental study on buoyancy-opposed wall jet in a confined space’, Int. J. of Heat and Fluid Flow, v23, pp487-496, 2002.
  14. S. He and J.D. Jackson 'A study of turbulence under conditions of transient flow in a pipe’, Journal of Fluid Mechanics, vol. 408, pp1-38, 2000.
4. Heat transfer to fluids at supercritical pressure

We have established a unified explanation for the laminarisation mechanisms in a heated pipe due to the variations of thermophysical properties, buoyancy and inertia, the last of which plays a significant role in a developing flow. In the new understanding, the various factors can all be treated similarly as (pseudo-)body forces, the effect of which is to cause a reduction in the so-called apparent Reynolds number (He et al 2021).

In addition we studied the flow of water at a supercritical pressure between parallel plates with heating/cooling on the two walls (DNS) - The project aims at developing a better understanding of the ‘direct effect of buoyancy’ and strong variations of thermal properties. DNS of flows in stably and unstably stratified flows and those in a vertical channel with fluids at supercritical are performed.

He J, Tian R, Jiang PX & He S (2021) Turbulence in a heated pipe at supercritical pressure. Journal of Fluid Mechanics, 920, A45. doi:10.1017/jfm.2021.458.

Instantaneous iso-surface graph
5. Fuel pin-brace interactions in an Advanced Gas-cooled Reactor (AGR)

Fuel pins rubbing braces that hold them in place due to flow turbulence is a current issue in some AGRs which causes fuel failures. This project aims at studying the vortex shedding generated at the end of the fuel rods and its impingement onto the downstream rods. Large Eddy Simulation (LES) has been carried out to investigate turbulent flow in an annular channel with streamwise inter-rod gapping.

The spacing between the rods is varied to study the effect of the mean flow as well as the turbulence structure revealing two distinct flow patterns analogous to the flow over the k-type and d-type roughness.

Fuel pin brace interactions

Fig. 1: the iso-surfaces of k2 of the instantaneous flow highlight the major differences exhibited in the flow structures in larger (6D) and smaller (2D) gap spacing. The former shows the vortical structures being ejected as a result of flow separation from the upstream rod and subsequently disappearing well before the downstream rod, where new strong vortical structures are generated as a result of the impinging flow on the rod and ensuing flow separation as the flow re-enters the annular space. By contrast, in the latter, the vortical structures produced upstream impact on the downstream rod overlapping the new structures produced locally. 

Reference: Kristin N. (2014), Numerical investigation of the flow structure in an annular channel with inter-rod spacing, PhD Thesis, University of Aberdeen.